Drawing with Fourier Series
Signal decomposition and reconstruction using DFT and Complex Fourier Series.
Applying the Discrete Fourier Transform (DFT) to a signal breaks it in its fundamental frequency components and their respective amplitudes. With this spectral information, the signal can be reconstructed using the Complex Fourier Series. This program performs both decomposition and reconstruction.
This program takes an svg image as input. It then creates some points that outlines the image.

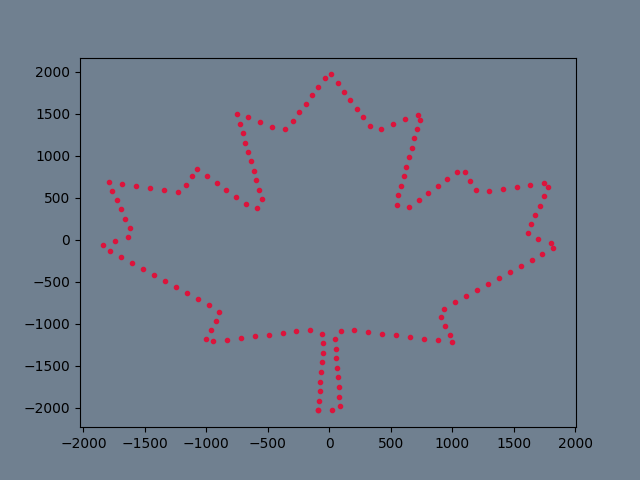
This outlined image is out discrete signal, and DFT is applied on it to get the fundamental frequencies present on this signal. We get this as a series of complex numbers, where the modulus of the complex number is the amplitude of the frequency, and the argument is the phase angle.
Once we have the spectral information of the signal, we can use that to perform different operations on the signal. We can use Complex Fourier Series to reconstruct the signal.
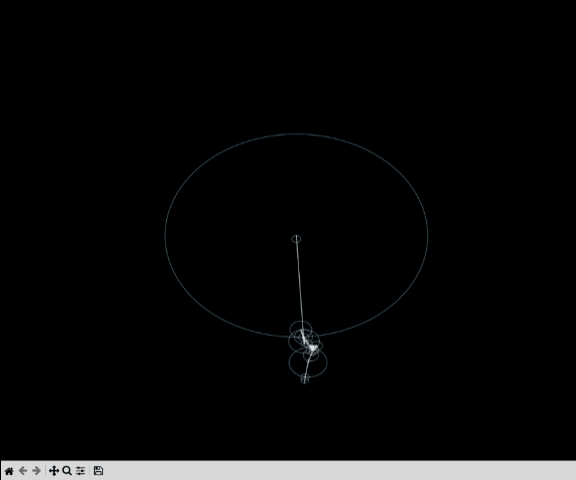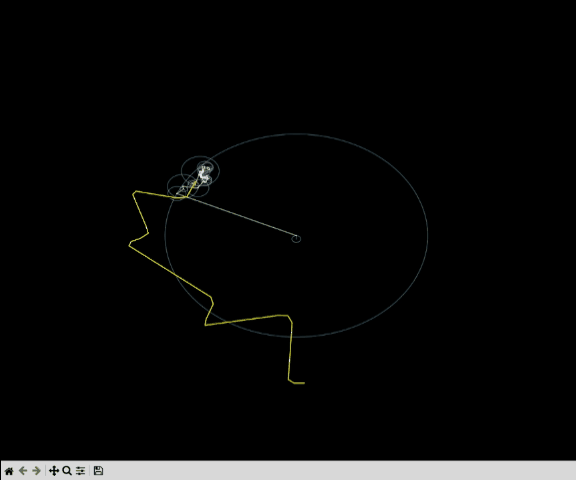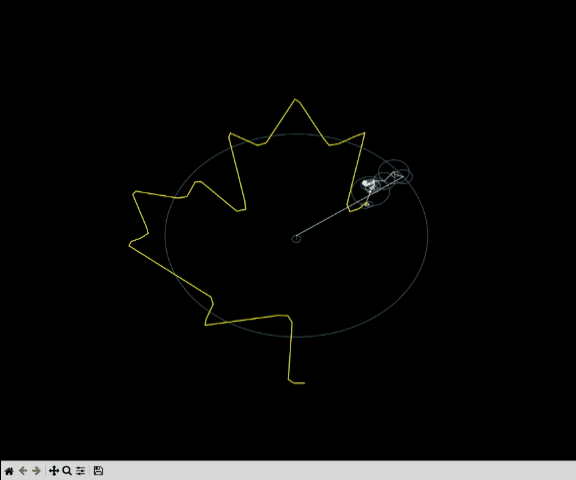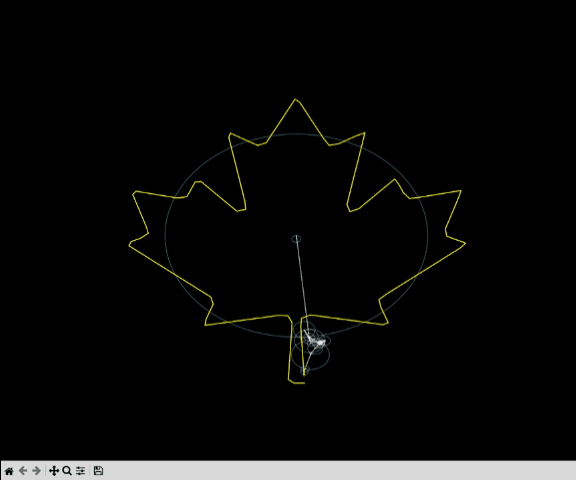
More about project and the code can be found here: Drawing with Fourier Series.
Learn more about:
- DFT: Drawing with Fourier Series.
- Complex Fourier Series: